１番

• ２つの選択肢があって、帰結が0/1であるときの決断方法について、ここなどで書いた
• 選択肢が[0,1]と連続値をとり、帰結も量的だとする
• ただし、選択肢の帰結は単純に平均と分散で決まる正規分布のようなものではなく、任意の分布であるとしよう
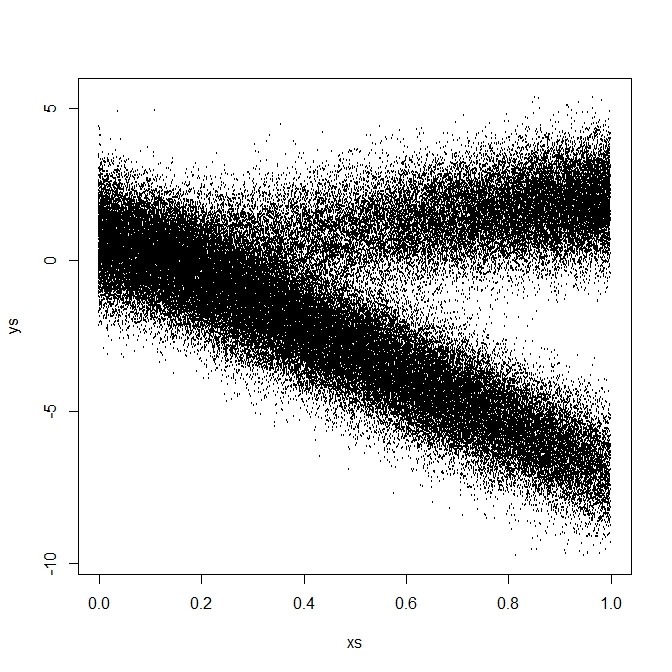
  • たとえばこんな感じ(横軸が選択肢、縦軸が帰結、個々の点が発生事象)

n.pt <- 100000

xs <- runif(n.pt)
m1 <- xs*2
m2 <- (0.6-xs)*8-3.8
p <- (xs-0.3)^2+0.2
ys <- rep(0,n.pt)
for(i in 1:n.pt){
	tmp1 <- rnorm(1,m1[i])
	tmp2 <- rnorm(1,m2[i])
	ys[i] <- sample(c(tmp1,tmp2),1,prob=c(p[i],1-p[i]))
}
plot(xs,ys,cex=0.1)

• 選択肢をどう選ぼうか、という問題なわけだけれど、分布の関数が与えられていたとして、連続値をとる選択肢について、ある値をとったときに、それ以外のすべての値をとったときとの比較で、そのある値の帰結が「１番」になる確率を、すべての選択肢について知りたいわけだけれど、どうしたらいよいのかわからない
• こんな風に考えてみる
• もし、選択肢が有限だったら、それぞれの選択肢について帰結の分布がわかっていれば、どの選択肢どれくらいの確率で１番になるかはわかるだろう
• 選択肢が連続値だというのは、選択肢数を無限大に飛ばせばよいので…
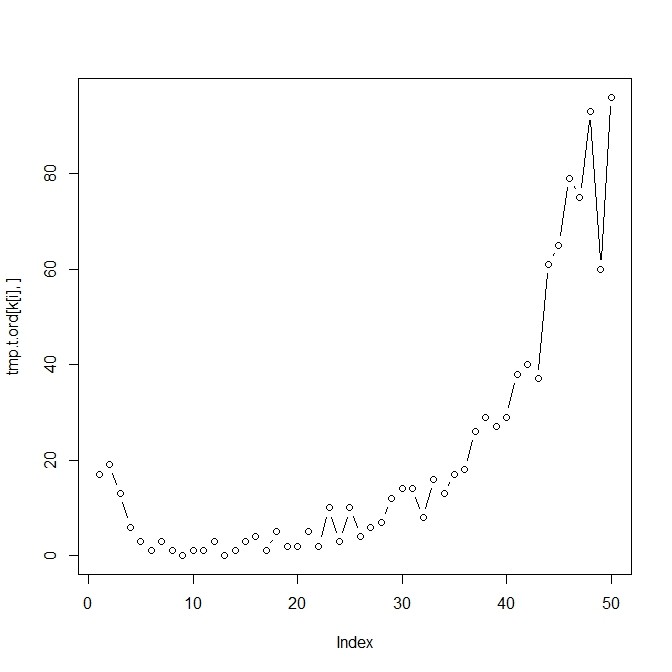
• リサンプリング法で行くと：
  • その結果はこれ…。ふーむ。

k <- 2:50
n.sample <- 1000
par(ask=FALSE)
for(i in 1:length(k)){
	tmp.x <- seq(from = 0, to = 1,length=k[i]+1)
	tmp.y <- list()
	for(j in 1:k[i]){
		selected <- which(xs>=tmp.x[j] & xs < tmp.x[j+1])
		tmp.y[[j]] <- ys[selected]
	}
	#tmp.z <- matrix(0,length(tmp.y),length(tmp.y))
	#for(j1 in 1:(length(tmp.y)-1)){
	#	for(j2 in (j1+1):length(tmp.y)){
	#		tmp.w <- outer(tmp.y[[j1]],tmp.y[[j2]],">")
	#		tmp.z[j1,j2] <- sum(tmp.w)/length(tmp.w)
	#	}
	#}
	#image(tmp.z)
	tmp.z2 <- matrix(0,length(tmp.y),length(tmp.y))
	
	tmp.w2 <- sapply(tmp.y,sample,n.sample,replace=TRUE)
	#tmp.ord <- apply(tmp.w2,1,order,decreasing=TRUE)
	tmp.ord <- apply(tmp.w2,1,rank,ties.method="max")
	tmp.t.ord <- apply(tmp.ord,1,tabulate,k[i])
	plot(tmp.t.ord[k[i],],type="b")
}

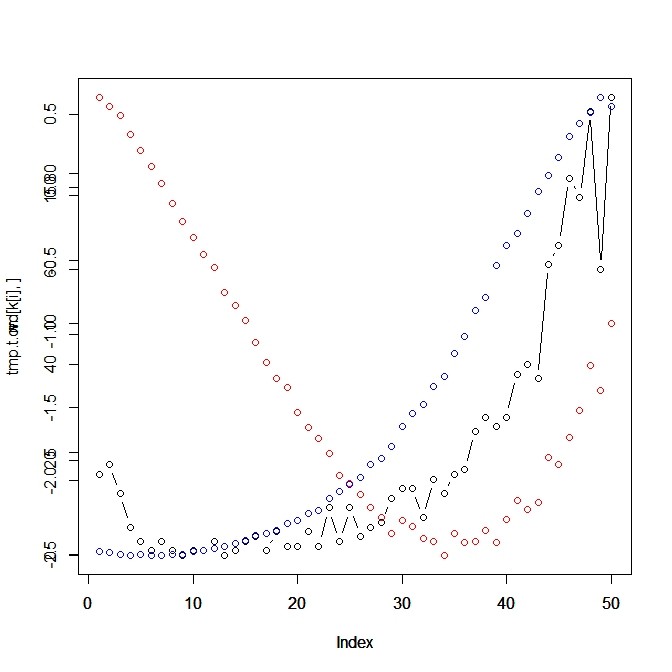
• • 平均と分散をかぶせてプロットしてみる(赤：平均、青：分散)

plot(tmp.t.ord[k[i],],type="b")
par(new=TRUE)
plot(m,col=2)
v <- sapply(tmp.y,var)
par(new=TRUE)
plot(v,col=4)