打ち切りのこと

• 生存解析の特徴と言えば、「打ち切りサンプル」があること
• また、イベントが発生するごとに、その後のイベントの生起を考えるための全体集団が小さくなっていくこと
• 生存曲線を描いて、曲線間に違いがあるかどうかを検定する方法としてログランクテスト・一般化ウィルコクソンがある(こちら)
  • ほぼ全員が死亡するまで解析する(打ち切りが少ない)と一般化ウィルコクソンとログランクとの差が大きくなるという
  • どのくらい大きくなるのだろう
• また、「ほぼ」ではなく、本当に「全員」が死亡するまで追跡したら、それは、「生存期間」に関する検定になる。たとえば、順序のある３カテゴリであれば、大雑把に言えば、順序カテゴリと生存時間について回帰をしてそれを検定してもよいかもしれない
  • では、これと、生存解析の検定とはどういう関係になるのだろうか
• やってみる
  • 一般化ウィルコクソンは青木先生の関数(こちら)
• 帰無仮説が成り立つ場合
  • ログランク・一般化ウィルコクソン・線形回帰のいずれも、p値は一様分布になるようだ

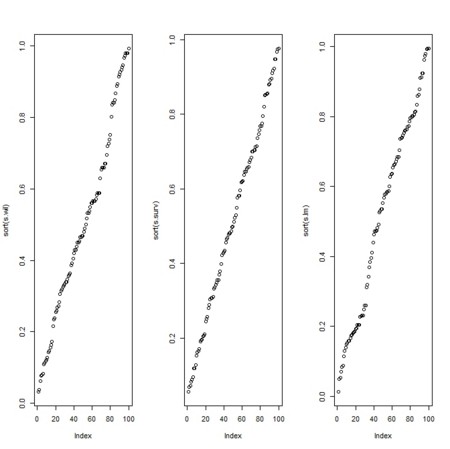
• • しかしながら、３つの手法のp値同士はばらばらなようだ(通常スケールとログスケールの２通りで示す)

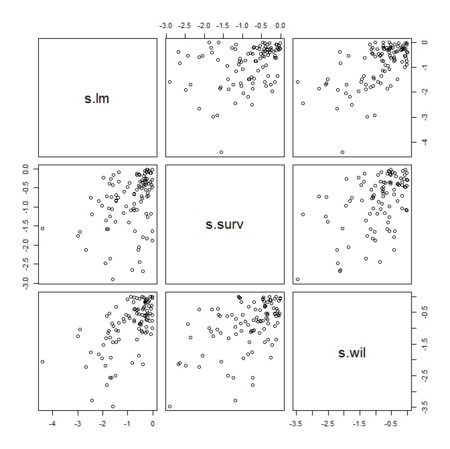
• 対立仮説が成り立つ場合にはどうだろうか
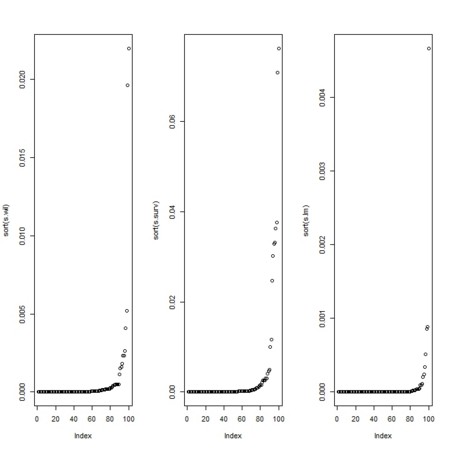
  • p値は小さい値に集中する
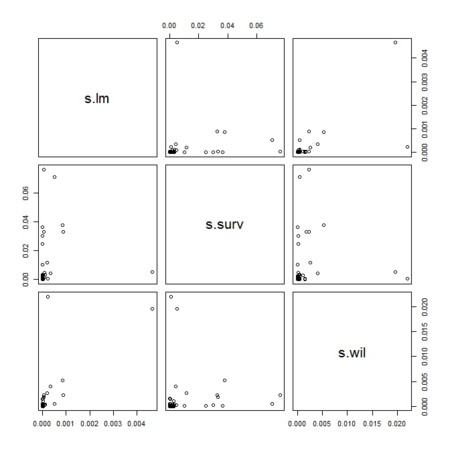
  • ３法の間には、それなりの相関が出てくる(が、結構ばらつきがある(軸のスケールが、線形回帰とログランクとでは同じだが、一般化ウィルコクソンでは異なることにも注意)

N<-100
t<-10+runif(N)*10
t<-sort(t)
p<-rep(1,N)
# k=Nなら帰無仮説をシミュレーションしていることになり
# k<Nなら対立仮説をシミュレーションしていることになる
k<-100
# k<-50
s<-sample(1:N,k)
g<-sample(1:3,N,replace=TRUE,prob=c(1/3,1/3,1/3))
g<-sort(g)
g1<-g
g1[s]<-sample(g[s])
plot(t,g)

Nperm<-100
s.lm<-s.surv<-s.wil<-rep(0,Nperm)

for(i in 1:Nperm){
	tmpg<-g
	tmps<-sample(1:N,k)

	tmpg[tmps]<-sample(g[tmps])
	s.lm[i]<-anova(lm(t~tmpg))[[5]][1]
	survout<-survdiff(Surv(t,p)~tmpg)
	s.surv[i]<-pchisq(survout[[5]],df=2,lower.tail=FALSE)
	wilout<-Gen.Wil(tmpg,p,t)
	s.wil[i]<-wilout$p.value
}
par(mfcol=c(1,3))
plot(sort(s.wil))
plot(sort(s.surv))
plot(sort(s.lm))

par(mfcol=c(1,1))

pairs(cbind(s.lm,s.surv,s.wil))
pairs(log(cbind(s.lm,s.surv,s.wil)))