2013-03-06

生存カーブ

生存解析

生存カーブが話題になった
生存カーブは
- 横軸が時間
- 縦軸が生存率
- カーブの傾きは「開始時刻の人口を基準とした、単位時間当たりの人口の減少率」
  - したがって、単位人口当たりの死亡率が一定のときには、カーブはだんだん緩やかになる
『誰がいつ死亡するかわからない』という状況を考えよう
- ２通りある
  - １つ目。常に死亡数/(単位時間・単位人数)が一定の場合
    - これは放射性同位元素の核崩壊と同じで、人口が指数関数的に減っていく

- - - 横軸は時間
    - 縦軸は生存率
    - カーブの傾きは単位時間当たりの(集団全体での)死亡人数(人口が減っているので、単位時間当たり・単位人数あたりの死亡人数は減っているので、だんだんに傾きが緩くなる)

n <- 10000
# すべて、死亡まで観察する
prob <- c(0,1)
censor <- sample(0:1,n,replace=TRUE,prob=prob)
# 指数乱数で死亡時刻が決まる
#times <- cumsum(rexp(n))
times <- sort(rexp(n))
x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
#par(mfcol = c(1,2))
#plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)

- - - このカーブの縦軸の対数をとると、「単位時間あたり・単位人数あたりの死亡数」を「傾き」としたカーブとなり、直線になる

plot(KMcurve$time,log(KMcurve$surv))

- - - 上述は脱落なしだったが脱落ありにすると、縦線が入って「脱落」を示すがカーブ自体は同じ

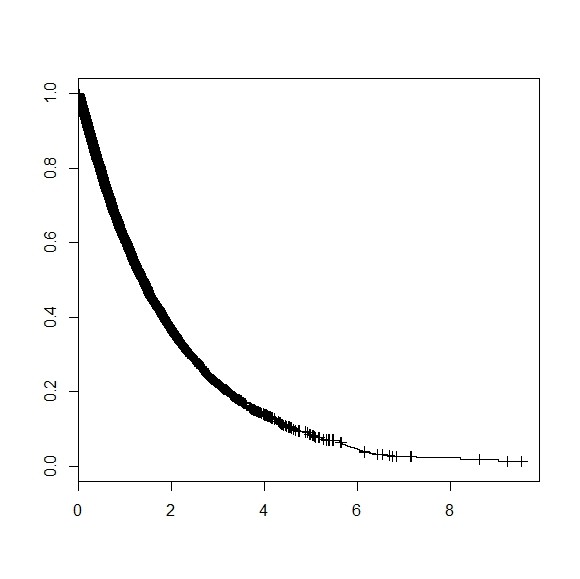
n <- 10000
# ランダムに脱落する
prob <- c(0.5,0.5)
censor <- sample(0:1,n,replace=TRUE,prob=prob)
# 指数乱数で死亡時刻が決まる
#times <- cumsum(rexp(n))
times <- sort(rexp(n))
x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
#par(mfcol = c(1,2))
#plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)

- - ２つ目。全員がある時間幅の中で死亡するが、いつ死亡するかわからないような状況
    - 単位時間当たりの集団全体での死亡数が一定である(単位人数あたりの死亡数は増えていく)
    - 『神のたたり』のせいで減っていく…みたいな
    - 村の人口が減るにしたがって「召される確率が上がっていく」

n <- 10000
# 全員、完全に追跡
prob <- c(0,1)
censor <- sample(0:1,n,replace=TRUE,prob=prob)
# ポツリポツリと起きること(ポアッソン過程)の事件の間隔は指数分布に従うので
# 指数乱数の累積和を生起時刻とする
times <- cumsum(rexp(n))
#times <- sort(rexp(n))
x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
#par(mfcol = c(1,2))
#plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)

- - - これの縦軸の対数をとると、「単位時間あたり・単位人数あたりの死亡数」を「傾き」としたカーブとなり、どんどん急になる

plot(KMcurve$time,log(KMcurve$surv))

- - - 脱落があると、人口が定速で減っていくのだが、脱落の影響で加速して減っているようなカーブになる

n <- 10000
# 全員、完全に追跡
prob <- c(0.5,0.5)
censor <- sample(0:1,n,replace=TRUE,prob=prob)
# ポツリポツリと起きること(ポアッソン過程)の事件の間隔は指数分布に従うので
# 指数乱数の累積和を生起時刻とする
times <- cumsum(rexp(n))
#times <- sort(rexp(n))
x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
#par(mfcol = c(1,2))
#plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)