2012-03-30

二値・非可逆フェノタイプで

R 時系列生存解析

昨日の記事で時間に関して離散的な観測データについて、そのまま・差分・累積をとり、それについて、統計量を作ってみることを書いた
今日の記事では、それを、良く知られた解析法が適用可能なデータ例に当てはめてみる
生存解析(「生死」を経時的に追跡するの)は、そのような例
- 生存解析についてはこちら)
以下では、「生死」をフェノタイプとせずに、「発病」をフェノタイプとして、「死亡」を追跡打ち切りとするような場合とする
２アレル型多型のジェノタイプが発病時期に影響するような場合
- ジェノタイプと発病・有病が関係する形式として、次のようなモデルを想定している
  - ジェノタイプが発病しやすさに影響することで、そのジェノタイプを保有している期間が長ければ長いほど、発病する
  - 言い換えると、すべての個人は発病するが、発病年齢が死亡よりも若ければ発病する、というモデル
- ジェノタイプ別の発病年齢(寿命が無限大である場合の仮の発病年齢)

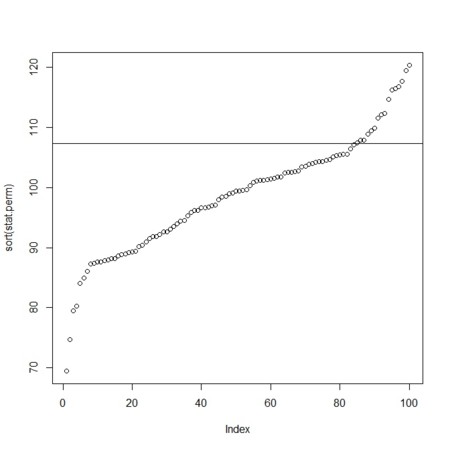
観測統計量とそのパーミュテーションによる統計量分布との関係

# 単純な遺伝因子の例
# allele freq
f<-0.3
# genotype freq
p<-c(f^2,2*f*(1-f),(1-f)^2)
# population
N<-100
# genotype of individuals
g<-sample(0:2,N,replace=TRUE,prob=p)
table(g)
# 時刻は年単位
t<-0:100
# 年齢
age<-sample(20:100,N,replace=TRUE)
# 発病年齢
a<-0
b<--10
tmp.onset<-round(20+exp(a+b*g+rnorm(N)*5))
tmp.onset<-100+b*g+round(rnorm(N)*10)
#tmp.onset<-rep(1000,N)
#tmp.onset[which(g==0)]<-rep(40,length(which(g==0)))
#tmp.onset[which(g==1)]<-rep(70,length(which(g==1)))
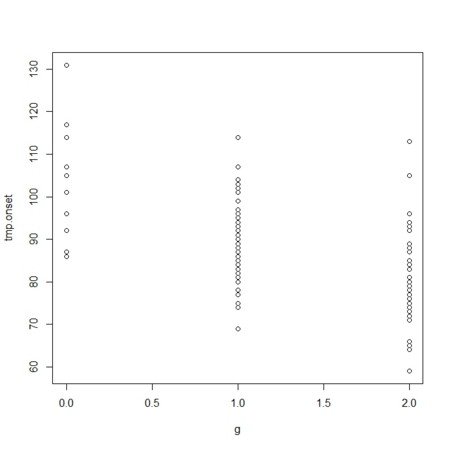
plot(g,tmp.onset)

# 生涯発症率
length(which(tmp.onset<=max(t)))/N

# ジェノタイプ
T1.list<-list()
for(i in 1:N){
	T1.list[[i]]<-list(time=c(0,round(age[i]/2),age[i]),value=rep(g[i],3))
}
# 疾患フェノタイプ
T2.list<-list()
for(i in 1:N){
	if(tmp.onset[i]<age[i]){
		tmp.time<-c(0,tmp.onset[i]-1,tmp.onset[i],age[i])
		tmp.value<-c(0,0,1,1)
		T2.list[[i]]<-list(time=tmp.time,value=tmp.value)
	}else{
		T2.list[[i]]<-list(time=c(0,round(age[i]/2),age[i]),value=rep(0,3))
	}
}


stat.ori<-0

for(i in 1:N){
	tmp<-my.TimeCorr(T1.list[[i]],T2.list[[i]],di1=-1,di2=1,perm=FALSE)
	stat.ori<-stat.ori+tmp$stat.ori
}

Nperm<-100
stat.perm<-rep(0,Nperm)
for(i in 1:Nperm){
	shG<-sample(g)
	for(j in 1:N){
		tmpT1<-T1.list[[j]]
		tmpT1$value<-rep(shG[j],3)
		tmpout<-my.TimeCorr(tmpT1,T2.list[[j]],di1=-1,di2=1,perm=FALSE)
		stat.perm[i]<-stat.perm[i]+tmpout$stat.ori
	}
}


plot(sort(stat.perm),ylim=range(stat.ori,stat.perm))
abline(h=stat.ori)

perm.p<-length(which(stat.perm>=stat.ori))/Nperm

- このデータを生存解析の枠組みにすれば以下の通り

# survival 解析のためにデータを作る
library(cmprsk)
# 観察時間
# 観察中に発病すれば1,発病せずに死亡すれば(打ち切れば)0

s.time<-rep(0,N)
s.censor<-rep(0,N)
s.group<-g
for(i in 1:N){
	if(tmp.onset[i]<age[i]){
		s.time[i]<-tmp.onset[i]
		s.censor[i]<-1
	}else{
		s.time[i]<-age[i]
	}
}
result <- survfit(Surv(s.time,s.censor) ~ s.group, type="kaplan-meier")
summary(result)

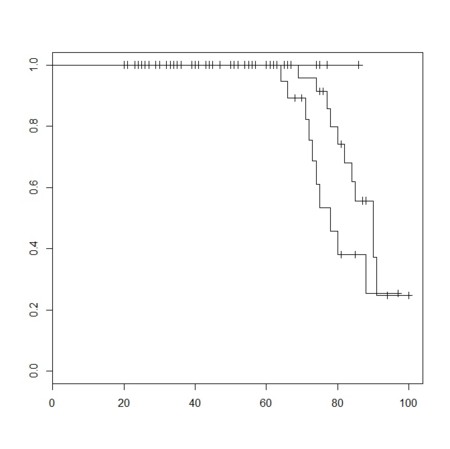
plot(result, conf.int=F)
survdiff(Surv(s.time,s.censor) ~ s.group)

# perm.pと比べる
perm.p

まったくもって、survdiff()　(これはログランクテスト)の結果と合わない
- 合わないことの一つの理由は、多人数からの統計量の算出がちょっとまずいのでは、ということ
- 合わないことのもう一つの理由は、こちらにあるように(ログランクと一般化ウィルコクソンとでも、相関が悪いし、そこに、線形回帰のようなものを入れても、やっぱり相関が悪いこと)と関係するのかもしれない
以下はいろいろ試してぐちゃぐちゃになったソース(自分以外に何の役にも立たないもの)

# 単純な遺伝因子の例
# allele freq
f<-0.3
# genotype freq
p<-c(f^2,2*f*(1-f),(1-f)^2)
# population
N<-100
# genotype of individuals
g<-sample(1:3,N,replace=TRUE,prob=p)
table(g)
# 時刻は年単位
t<-0:100
# 年齢
age<-sample(90:100,N,replace=TRUE)
# 発病年齢
a<-80
b<--10
tmp.onset<-round(20+exp(a+b*g+rnorm(N)*5))
tmp.onset<-100+b*g+round(rnorm(N)*10)
#tmp.onset<-rep(1000,N)
#tmp.onset[which(g==0)]<-rep(40,length(which(g==0)))
#tmp.onset[which(g==1)]<-rep(70,length(which(g==1)))
plot(g,tmp.onset)

# 生涯発症率
length(which(tmp.onset<=max(t)))/N

# ジェノタイプ
T1.list<-list()
for(i in 1:N){
	T1.list[[i]]<-list(time=c(0,round(age[i]/2),age[i]),value=rep(g[i],3))
}
# 疾患フェノタイプ
T2.list<-list()
for(i in 1:N){
	if(tmp.onset[i]<age[i]){
		tmp.time<-c(0,tmp.onset[i],age[i])
		tmp.value<-c(0,1,1)
		T2.list[[i]]<-list(time=tmp.time,value=tmp.value)
	}else{
		T2.list[[i]]<-list(time=c(0,round(age[i]/2),age[i]),value=rep(0,3))
	}
}

library(cmprsk)
# 観察時間
# 観察中に発病すれば1,発病せずに死亡すれば(打ち切れば)0

s.time<-rep(0,N)
s.censor<-rep(0,N)
s.group<-g
for(i in 1:N){
	if(tmp.onset[i]<age[i]){
		s.time[i]<-tmp.onset[i]
		s.censor[i]<-1
	}else{
		s.time[i]<-age[i]
	}
}

stat.ori<-0

for(i in 1:N){
	tmp<-my.TimeCorr(T1.list[[i]],T2.list[[i]],di1=0,di2=1,perm=FALSE)
	print(tmp)
	stat.ori<-stat.ori+tmp$stat.ori
}

Nperm<-100
stat.perm<-surv.perm<-wil.perm<-rep(0,Nperm)
for(i in 1:Nperm){
	shG<-sample(g)
	for(j in 1:N){
		tmpT1<-T1.list[[j]]
		tmpT1$value<-rep(shG[j],3)
		tmpout<-my.TimeCorr(tmpT1,T2.list[[j]],di1=0,di2=1,perm=FALSE)
		stat.perm[i]<-stat.perm[i]+tmpout$stat.ori
		
	}
	tmp.s.group<-shG
	out.surv<-survdiff(Surv(s.time,s.censor) ~ tmp.s.group)
	surv.perm[i]<-out.surv[[5]]
	tmpWil<-Gen.Wil(tmp.s.group,s.censor,s.time)
	wil.perm[i]<-tmpWil$p.value

}


plot(sort(stat.perm),ylim=range(stat.ori,stat.perm))
abline(h=stat.ori)

perm.p<-length(which(stat.perm>=stat.ori))/Nperm
plot(stat.perm,wil.perm)



# survival 解析のためにデータを作る
library(cmprsk)
# 観察時間
# 観察中に発病すれば1,発病せずに死亡すれば(打ち切れば)0

s.time<-rep(0,N)
s.censor<-rep(0,N)
s.group<-g
for(i in 1:N){
	if(tmp.onset[i]<age[i]){
		s.time[i]<-tmp.onset[i]
		s.censor[i]<-1
	}else{
		s.time[i]<-age[i]
	}
}
result <- survfit(Surv(s.time,s.censor) ~ s.group, type="kaplan-meier")
summary(result)
surv.perm<-stat.perm2
wil.perm<-stat.perm2

plot(result, conf.int=FALSE)
survdiff(Surv(s.time,s.censor) ~ s.group)

# perm.pと比べる
perm.p


# 簡易計算でやってみる
stat.ori2<-sum(s.time*s.censor*s.group)
stat.ori3<-sum(1/s.time*s.censor*s.group)
Nperm2<-Nperm3<-100
stat.perm2<-rep(0,Nperm2)
stat.perm3<-stat.perm2
surv.perm<-stat.perm2
wil.perm<-stat.perm2
for(i in 1:Nperm2){
	tmp.s.group<-sample(s.group)
	stat.perm2[i]<-sum(s.time*s.censor*tmp.s.group)
	stat.perm3[i]<-sum(1/s.time*s.censor*tmp.s.group)
	out.surv<-survdiff(Surv(s.time,s.censor) ~ tmp.s.group)
	surv.perm[i]<-out.surv[[5]]
	tmpWil<-Gen.Wil(tmp.s.group,s.censor,s.time)
	wil.perm[i]<-tmpWil$p.value
}

plot(sort(stat.perm2),ylim=range(stat.ori2,stat.perm2))
abline(h=stat.ori2)

perm.p2<-length(which(stat.perm2>=stat.ori2))/Nperm2

plot(sort(stat.perm3),ylim=range(stat.ori3,stat.perm3))
abline(h=stat.ori3)

perm.p3<-length(which(stat.perm3>=stat.ori3))/Nperm3

plot(stat.perm2,wil.perm)

plot(surv.perm,wil.perm)