Levy過程

• Levy過程が数学セミナーの2012年6月号で扱われている
• Levyと言えば、レヴィ飛行についてはこちらに少しだけ書いた
• 少し整理しよう
  • 参考にした資料1
  • 参考にした資料2
• 整理した上で、確率過程と生物学（遺伝統計学）との関係についても考えてみることにする
• Levy過程は確率過程に含まれる
• Levy飛行はLevy過程に含まれる
• したがって、まずは確率過程から
• 確率過程 Stochastic process
  • とりうる状態が複数あって、その状態のどれかが選ばれることが確率的な Stochastic
  • 時間に伴う変化が過程 process
• 確率空間と状態空間
  • 取りうる状態とその選ばれ方は、確率空間と状態空間という２つの空間で考える
  • 現象が起きて、観察される。その観察されるもの(こと)が状態空間
  • 確率空間は確率変数があって、確率変数が取りうる値の集合
  • ２つの空間(確率空間と状態空間)の間には対応関係がある
  • 例
    • サイコロを振って、偶数なら前進、奇数なら後退するとき、サイコロの目「1,2,3,4,5,6」が確率空間(の全事象)、サイコロの目の出る出やすさが確率分布、前進・後退する道が状態空間。確率空間(サイコロの目)３通りに、状態空間(道)の１歩の方向が対応している。確率空間と状態空間(の変化)には対応関係がある
• 確率過程の分類(こちら)
  • 状態と時間とについて４分類される
    • (1)状態が離散的、時間も離散的
    • (2)状態が離散的、時間が連続
    • (3)状態が連続、時間が離散的
    • (4)状態が連続、時間も連続
• 確率過程を表現するパーツ
  • 確率空間は可測空間。次の２つが必要
    • 事象集合
    • 事象集合を可測に定めるルール
  • 確率空間には、「全体」で１になる確率密度分布がある
  • 以上の３つ。事象集合(の全体)、可測にするルール、密度分布
  • 状態空間
    • 空間(ユークリッド空間だったり、多様体だったり、いろいろ)
  • 過程を表す関数
    • 確率空間と状態空間とを結び、時刻ごとに状態のとりかたを確率的に定めるもの
• Levy過程(Wiki)
  • Levy過程は確率過程の一つ
  • 「変化の仕方」がいつも同じ
  • 「変化」して移動した先でも、「変化の仕方」は同じ
  • したがって、状態空間は、どこも「均一」である必要がありそうだ
  • Levy過程を決めるのは・・・
    • 確率空間(全体集合、可測に定めるルール、その上の確率密度関数)
    • 状態空間
    • 確率空間と状態空間を結ぶ関数
  • 「確率密度関数」を変えると状態変化の様相が変わる
    • たとえばLevy飛行では、確率密度関数の変数を変えることで飛行の軌跡の様子が変わっている(Wiki)

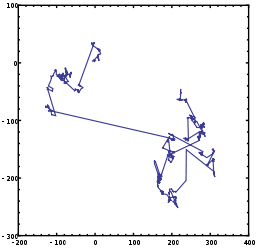
• • • • Figure 1. An example of 1000 steps of a Lévy flight in two dimensions. The origin of the motion is at [0,0], the angular direction is uniformly distributed and the step size is distributed according to a Lévy (i.e. stable) distribution with α = 1 and β = 0 which is a Cauchy distribution. Note the presence of large jumps in location compared to the Brownian motion illustrated in Figure 2.

• • • • Figure 2. An example of 1000 steps of an approximation to a Brownian motion type of Lévy flight in two dimensions. The origin of the motion is at [0, 0], the angular direction is uniformly distributed and the step size is distributed according to a Lévy (i.e. stable) distribution with α = 2 and β = 0 (i.e., a normal distribution).
• 生物と確率過程
  • 生物の定常状態
    • 確率過程だとする
    • 「状態空間」が動ける範囲で一様であるならば、Levy過程になっている(？）
    • Levy過程の特徴は確率密度関数(のパラメタ)が決めているから、確率密度関数(のパラメタ)に影響する因子(環境因子・遺伝因子)はLevy過程の特徴に影響を与える
    • Levy過程の特徴に影響を与えるとき、それは、とりやすい状態そのものを選ばせているというよりは、状態空間の移動の特徴を決めている
    • したがって、「とっている状態」と因子との関係は(相当に)間接的な関係しかとらない
  • 生物は予定軌道を持っている
    • 発生・成長・老・死と、予定軌道を持っている
    • これは、一様な状態空間におけるLevy過程では説明できない
    • 一見、Levy過程様に見えることもあるが、それは「多様体の局所」はユークリッド空間に見えるのといっしょで、大局的には、「流路の決まった多様体上の移動」になっている
    • 定常状態は、局所での安定を見ているだけ
    • この「予定軌道」を持った多様体を決めているのが、「プログラム」
  • 生物は１個体の予定軌道(単為生殖なら１つの予定軌道から、有性生殖なら２つの予定軌道から)から別の予定軌道を発芽する仕組みを持っている
  • 多細胞生物のこと
    • 多細胞生物の個々の細胞に着目し、それを単細胞生物になぞらえれば、多細胞生物というのは、多細胞の中に、堅固な相互干渉ルールがある状態と言える
    • 確率過程が個々の細胞で決まっているのではなく、確率過程間の相互作用という「メタ」な確率過程になっている
  • 「メタ」な確率過程
    • 個体がたくさん集まって、複数個体のそれぞれの確率過程が相互に「メタ」な確率過程を作るのも特徴
  • 多層的な階層的相互作用型確率過程も生命現象に特徴的