検定p値と検定統計量

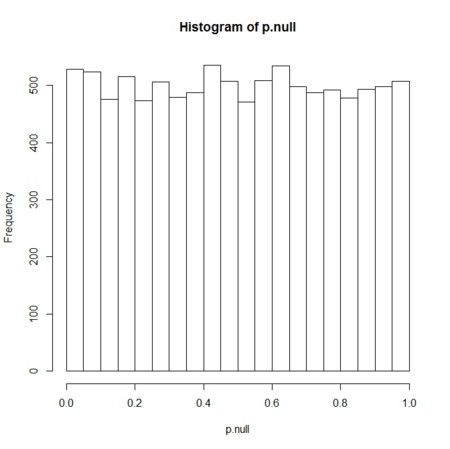
• 帰無仮説が成り立つ仮説検定のp値
  • 一様分布。小さいp値も大きいp値も同じくらい頻繁に得られる、同じくらい珍しく得られる

p.null <- runif(10000)
hist(p.null)

• p値の独立・非独立と検定統計量の独立・非独立
  • ２つの検定のp値が独立であるということは、片方のp値が小さくても大きくても、もう片方のp値の分布に変化がない

p1.null <- runif(10000)
p2.null <- runif(10000)
plot(p1.null,p2.null,cex= 0.001)

• • ２つの検定が非独立なときは、片方のp値が小さいときにはもう片方のp値が一様分布ではなく、小さい方に偏っていたり、大きい方に偏っていたり、とにかく一様ではない
  • こんな偏り方もある。p1.null,p2.null自体は一様分布だが、両者は独立ではない

p1.null <- runif(10000)
p2.null <- runif(10000)
s.p1.null <- sort(p1.null)
s.p2.null <- sort(p2.null)
s.p2.null.2 <- c(sample(s.p2.null[1:(length(s.p2.null)/2)]),sample(s.p2.null[(length(s.p2.null)/2+1):length(s.p2.null)]))
plot(s.p1.null,s.p2.null.2)

• • このようなp1,p2が自由度１のカイ自乗統計量から出たものだとすると、カイ自乗統計量同士の非独立な具合はこんな感じ

plot(qchisq(s.p1.null,1),qchisq(s.p2.null.2,1),cex=0.01)

• • カイ自乗統計量は、「距離の２乗」と言えるような値なので、自由度１のカイ自乗統計量の関係性の深さは角度で表すことができる
  • ２つの統計量の独立・非独立(それが表すp値の独立・非独立)の一つの例として次のような２つのカイ自乗統計量を取ることにする
    • ２次元正規分布をとるような事象があり、２つのカイ自乗統計量を２つの単位ベクトルとの内積の２乗で定義する。この２つの単位ベクトルのなす角が直角のとき、２つの統計量は独立であり、それ以外のときには、角の大きさに従って非独立の程度が定まる
  • ２次元正規分布

X <- matrix(rnorm(10000*2),ncol=2)
mm <- max(abs(X))
plot(X,xlim= c(-mm,mm),ylim=c(-mm,mm))

• ２つの単位ベクトルはこんな感じ

mm <- max(abs(X))
plot(X,xlim= c(-mm,mm),ylim=c(-mm,mm),cex=0.01)

phi <- pi/6
v1 <- c(cos(-phi/2),sin(-phi/2))
v2 <- c(cos(phi/2),sin(phi/2))

arrows(0,0,v1[1],v1[2],code = 2,col=2,lwd = 3)
arrows(0,0,v2[1],v2[2],code = 2,col=3,lwd = 3)

• • ちなみに、２ベクトルが直交しているときは