2013-02-17

対立仮説に分布を想定したときのPPV

対立仮説分散インフレーションパワー PPV FDR ジェノミックコントロール R

こちらの続き
普通の場合(１つの帰無仮説と１つの対立仮説を想定した場合)
- 帰無仮説ではm.null、対立仮説ではm.altであるとする
- 今から、調べようとしているのだが、帰無仮説が成り立つ確率をpnull、対立仮説が成り立つ仮説をpalt (pnull + palt = 1)と考えているとする(事前確率)
- その様子を絵で描くとこんな感じ(黒と赤の長さの和は１)

# 仮説の「強さ」を表すパラメタ
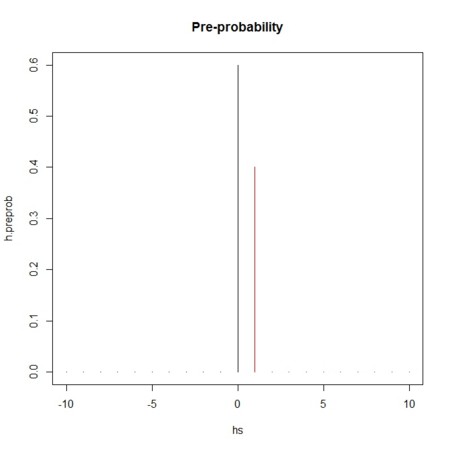
hs <- seq(from=-10,to=10,by=1)
# 検討する値の範囲、台
x <- seq(from=-10,to=10,by=0.01)
# 帰無仮説と対立仮説を表す値
m.null <- 0
m.alt <- 1
# 仮説の強さはいろいろな値をとるが、この値を境として「意味のある関連」「意味がない関連〜帰無とみなす」の２群に分ける。そんな閾値
alt.v <- m.alt-0.1
# 検定するときの陽性・陰性のカットオフ値
cut.v <- m.alt/2
# 「意味のある関連はない〜帰無仮説相当」は黒、「意味のある関連がある〜対立仮説相当」は赤
col <- rep(1,length(hs))
col[which(hs>=alt.v)] <- 2
h.preprob <- rep(0,length(hs))
pnull <- 0.6
palt <- 1-pnull
h.preprob[which(hs==m.null)] <- pnull
h.preprob[which(hs==m.alt)] <- palt
plot(hs,h.preprob,type="h",main = "Pre-probability",col = col)

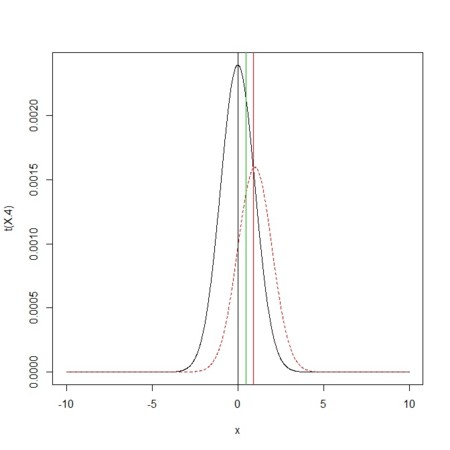
ここで実際にデータを取ると、帰無仮説の場合に統計量が正規分布をとり、対立仮説も正規分布を取って、以下に示すようになる
- 帰無仮説・対立仮説の場合のそれぞれの正規分布が黒・赤で描かれている。２つの正規分布の下面積はそれぞれpnullとpaltである。足し合わせると、もちろん、１。カットオフが緑の垂直線。

s <- 1

X <- matrix(0,length(hs),length(x))

for(i in 1:length(hs)){
	tmp <- dnorm(x,hs[i],s)
	X[i,] <- tmp/sum(tmp) * h.preprob[i]
}
matplot(x,t(X),type="l",col=col)
abline(v=m.null,col=1)
abline(v=alt.v,col=2)
abline(v=cut.v,col=3)
X.4 <- matrix(0,2,length(x))
for(i in 1:length(hs)){
	X.4[col[i],] <- X.4[col[i],] + X[i,]
}

matplot(x,t(X.4),type="l",col=c(1,2))
abline(v=m.null,col=1)
abline(v=alt.v,col=2)
abline(v=cut.v,col=3)

閾値cut.vを定めれば、帰無仮説が成り立っていて、かつ、陰性の確率(黒の正規分布で緑より左側の下面積:BL)、帰無仮説が成り立っていて、かつ、陽性の確率(黒の正規分布で緑より右側の下面積:BR)、対立仮説が成り立っていて、かつ、陰性の確率(赤の正規分布で緑より左側の下面積:RL)、対立仮説が成り立っていて、かつ、陽性の確率の４つの確率(赤の正規分布で緑より右側の下面積:RR)が求められる(その和は１)
2x2表
- BL,BR
- RL,RR
を作る
- BL + BR = pnull = 0.6
- RL + RR = palt = 0.4 になっている

two.by.two.1 <- matrix(0,2,2)
for(i in 1:length(x)){
	if(x[i] <= cut.v){
		two.by.two.1[,1] <- two.by.two.1[,1] + X.4[,i]
	}else{
		two.by.two.1[,2] <- two.by.two.1[,2] + X.4[,i]
	}
}
two.by.two.1

> two.by.two.1
          [,1]      [,2]
[1,] 0.4159328 0.1840672
[2,] 0.1241197 0.2758803

- 感度・パワーはRR/(RL + RR)
- 特異度はBL/(BL+BR)
- タイプ１エラーはBR/(BL+BR)
- タイプ２エラーはRL/(RL+RR)
- 陽性の場合に、対立仮説が占める割合 PPV はRR/(RR+BR)
- 陽性の場合に、帰無仮説が占める割合 FDR はBR/RR+BR)

m1.1 <- apply(two.by.two.1,1,sum)
m2.1 <- apply(two.by.two.1,2,sum)
sens.spec.1 <- t(t(two.by.two.1)/m1.1)
sens.spec.1
ppv.fdr.1 <- two.by.two.1/m2.1
ppv.fdr.1

- 実際、感度・パワーは0.6897、特異度は0.6932、タイプ１エラーは0.4602、タイプ２エラーは0.2369、PPVは0.5998、FDRは0.3408

> two.by.two.1
          [,1]      [,2]
[1,] 0.4159328 0.1840672
[2,] 0.1241197 0.2758803

> sens.spec.1
          [,1]      [,2]
[1,] 0.6932213 0.4601680
[2,] 0.2068662 0.6897007
> ppv.fdr.1 <- two.by.two.1/m2.1
> ppv.fdr.1
          [,1]      [,2]
[1,] 0.7701710 0.3408320
[2,] 0.2698563 0.5998082

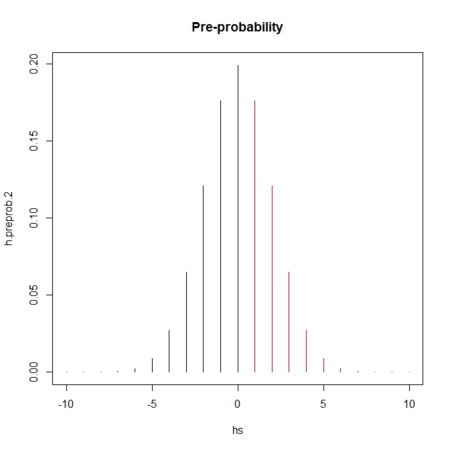
ここで、帰無仮説・対立仮説を連続的な分布にしてみる
- 離散的なグラフにしてあるが、なめらかにつながっているものとする
- 黒は、「意味のあるような関連はない〜帰無仮説とみなせるような仮説」、赤は「意味のある関連がある〜対立仮説とみなせるような仮説」

s2 <- 2
h.preprob.2 <- dnorm(hs,0,s2)
h.preprob.2 <- h.preprob.2/sum(h.preprob.2)
plot(hs,h.preprob.2,type="h",main = "Pre-probability",col = col)

これについて同様の処理を行う

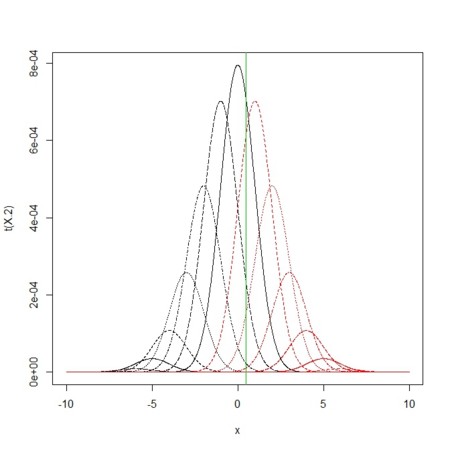
- いくつかの仮説だけを取り出して、その仮説について観察される統計量の分布を描いている。仮説の事前確率に応じて、下面積は小さくなっている。また、黒と赤の意味は「帰無仮説相当」「対立仮説相当」のことである
- もとの仮説の分布よりも、仮説に基づいてばらつきを持って観察される統計量分布は、幅広の分布となっている。分散がインフレーションしている(〜この幅広になる具合がジェノミックコントロールの分散インフレに相当する)
- 検定のカットオフの緑の線とそれぞれの仮説の位置関係を見れば、「帰無仮説相当」かつ緑線より右・左、「対立仮説相当」かつ緑線より右・左、という分け方ができる

s <- 1

X.2 <- matrix(0,length(hs),length(x))

for(i in 1:length(hs)){
	tmp <- dnorm(x,hs[i],s)
	X.2[i,] <- tmp/sum(tmp) * h.preprob.2[i]
}
matplot(x,t(X.2),type="l",col=col)
#abline(v=m.null,col=1)
#abline(v=alt.v,col=2)
abline(v=cut.v,col=3)

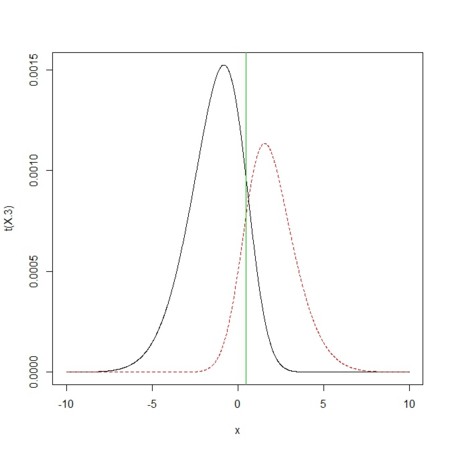
たくさんの分布が重なっていると見にくいので、「帰無仮説相当」と「対立仮説相当」とでまとめて描くこととする

- 黒・赤の２つの分布が得られて、その下面積の和は１であり、また、それぞれの分布曲線の下面積は、「帰無仮説相当」の事前確率、「対立仮説相当」の事前確率となる
- また、気づくことは、黒の分布のピークは0よりも左に寄っていること、赤の分布のピークは相対的に右にシフトしていることである(これは、全体の分布が0を中心に左右対称であったところを、片方側だけをとりのけたからである

X.3 <- matrix(0,2,length(x))
for(i in 1:length(hs)){
	X.3[col[i],] <- X.3[col[i],] + X.2[i,]
}

matplot(x,t(X.3),type="l",col=c(1,2))
#abline(v=m.null,col=1)
#abline(v=alt.v,col=2)
abline(v=cut.v,col=3)

ここから、2x2表を作るのも同じことで、感度・特異度・PPV・FDRの算出も同じ
- 感度・パワーは0.8421、特異度は0.87729、タイプ１エラーは0.1839、タイプ２エラーは0.0632、PPVは0.82078、FDRは0.1249

two.by.two <- matrix(0,2,2)
for(i in 1:length(x)){
	if(x[i] <= cut.v){
		two.by.two[,1] <- two.by.two[,1] + X.3[,i]
	}else{
		two.by.two[,2] <- two.by.two[,2] + X.3[,i]
	}
}
two.by.two

m1 <- apply(two.by.two,1,sum)
m2 <- apply(two.by.two,2,sum)
sens.spec <- t(t(two.by.two)/m1)
sens.spec
ppv.fdr <- two.by.two/m2
ppv.fdr

> two.by.two
           [,1]       [,2]
[1,] 0.52613995 0.07359563
[2,] 0.06319832 0.33706610

> sens.spec
          [,1]      [,2]
[1,] 0.8772865 0.1838675
[2,] 0.1053770 0.8421086
> ppv.fdr <- two.by.two/m2
> ppv.fdr
          [,1]      [,2]
[1,] 0.8927639 0.1248784
[2,] 0.1538939 0.8207877