ちょっと違う分布

• こんな分布がある

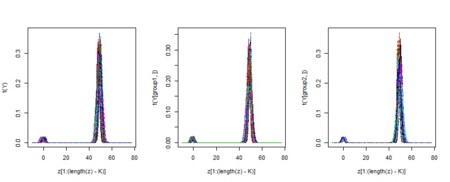
• 左は全サンプルの分布、中央と右は群１・群２の分布
• 群１と群２の間で違っているだろうか？
• シミュレーションでは、分布の左にある小さいコブの位置が少し違えてある
• シミュレーションでは、２峰性の分布の横軸が(実験系の影響で)ぶれることを想定している
• お試しソース

n.r <- 100

ps <- rep(0,n.r)

for(rr in 1:n.r){

m1 <- c(0,1)
m2 <- c(50,50)

p <- 0.05

n <- 100

z <- seq(from=-10,to=80,length=100)
K <- 3
X <- cbind(sample(1:2,n,replace=TRUE),runif(n)+1,sample(1:K,n,replace=TRUE))
#X[,2] <- X[,2] + X[,1]
Y <- matrix(0,n,length(z)-K)
for(i in 1:n){
	Y[i,] <- (p*dnorm(z,m1[X[i,1]]+rnorm(1,0,0.3),1)+(1-p)*dnorm(z,m2[X[i,1]]+rnorm(1,0,0.3),X[i,2]))[X[i,3]:(X[i,3]+(length(z)-K-1))]
}

group1 <- which(X[,1]==1)
group2 <- which(X[,1]==2)


par(mfcol=c(1,3))
matplot(z[1:(length(z)-K)],t(Y),type="l")
matplot(z[1:(length(z)-K)],t(Y[group1,]),type="l")
matplot(z[1:(length(z)-K)],t(Y[group2,]),type="l")
par(mfcol=c(1,1))

Y.rsum <- apply(t(t(Y)*z[1:(length(z)-K)]),1,sum)
mean.Y<-list(Y.rsum[group1],Y.rsum[group2])

boxplot(mean.Y)
t.test(mean.Y[[1]],mean.Y[[2]])


D <- matrix(0,n,n)
for(i in 1:n){
	for(j in 1:n){
		D[i,j] <- sum(Y[i,] * log(Y[i,]/Y[j,]))
	}
}

image(D)

image(D[c(group1,group2),c(group1,group2)])

S.ori <- sum(D[group1,group1])+sum(D[group2,group2])

n.iter <- 1000
S.perm <- rep(0,n.iter)
for(i in 1:n.iter){
	tmp.X <- sample(X[,1])
	tmp.group1 <- which(tmp.X==1)
	tmp.group2 <- which(tmp.X==2)
	S.perm[i] <- sum(D[tmp.group1,tmp.group1])+sum(D[tmp.group2,tmp.group2])
}

plot(c(sort(S.perm),S.ori))
abline(h=S.ori)
ps[rr] <- length(which(S.perm < S.ori))/n.iter
}
hist(ps)
plot(sort(ps))