2014-03-27

カーネル推定のオーダー

こちらでGaussian Sequence Modelをなぞっている。その一環
カーネル関数にはオーダーというものがあって、畳みこんでスムージングするときのバイアス制御と関係するという話があり、それを用いて話が進んで行くのだが、ぼんやりしているので、確認しておく
参考はこちら
まず、カーネル関数は、台全体での積分が1である。確率密度関数とこの点は同様だが、確率密度関数が非負であるのに対して、カーネル関数の値は負でもよい
- $\int_{-\infty}^{\infty} k(v) dv = 1$
カーネル関数の0周りのp次モーメント $\mu_p=\int_{-\infty}^{\infty} v^p k(v) dv$ によってカーネル関数を特徴分類する
上記のように $\mu_0 = 1$
（後述のように・後述しないかもしれないけれど）カーネル関数のモーメントは、カーネル推定において、バイアスと関連しているので、0であるモーメントが多いと便利である
そのため、 $\mu_1 = 1$ であるようなカーネルは大事。これは、「平均が0」ということ。逆に言うと、これはバイアス制御上大事なので、0周りのp次モーメントを考える代わりに $\mu_1$ 周りのモーメントを考えることが多い。それはカーネル関数の形を変えずにシフトするだけ。したがって、カーネル関数の形に本質的に影響しない
それ以外でp次モーメントに0のものを持ち出すには、0周り（ $\mu_1=0$ 周り）で対称な関数を考えることである。対称な関数では奇数次モーメントがすべて0になる。したがって、対称関数は都合がよい
というわけで対称なカーネル関数を考える
対称なカーネル関数の奇数次モーメントは0であるから、さらなる分類をするとなると、偶数次モーメントが0か否かに注目することになる。
q-thオーダーモーメント関数と言うとき、q未満のすべてのモーメントが0であるような関数であると言うことにする
- 対称関数ではqには偶数のみが適合し、2-th orderカーネル,4-th orderカーネル…となる
ちなみに、非負の値しかとらないカーネル関数では、 $\mu_2 > 0$ であるから、必ず2nd order カーネルとなる
2nd order カーネルの例
- Uniform $k_0(v) = \frac{1}{2} \text{when } |v| \le 1$
- Epanchnikov $k_1(v) = \frac{3}{4}(1-u^2) \text{when } |v| \le 1$
- Boweight $k_2(v) = \frac{15}{16}(1-u^2)^2 \text{when } |v| \le 1$
- Triweight $k_3(v) = \frac{35}{32}(1-u^2)^3 \text{when } |v| \le 1$
- Gaussian $k_{gauss}(v) = \frac{1}{\sqrt{2 \pi}}exp^{-\frac{v^2}{2}}$

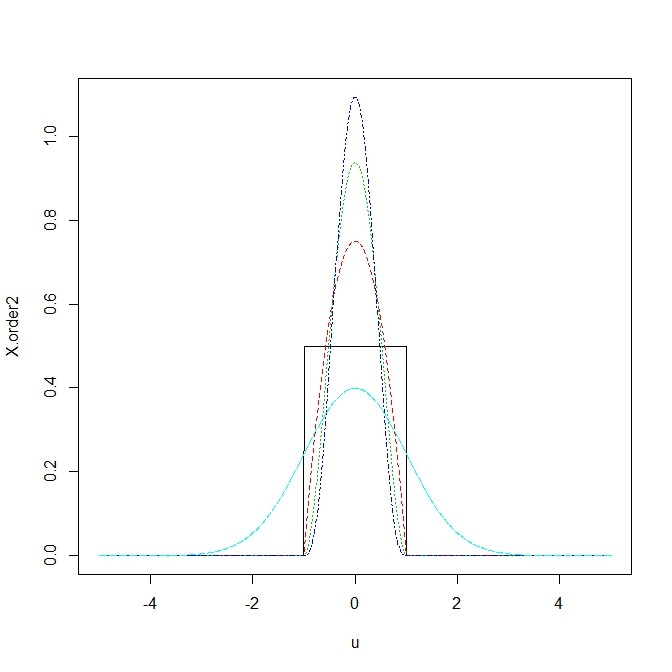
じゃあ4-th orderカーネルは…
- 2nd orderカーネルの周辺部に負の領域を抱き込ませた形
- Epanchnikov $k_{4,1}(v) = \frac{15}{8})(1-\frac{7}{3}v^2)\times k_1(v)$
- Biweight $k_{4,2}(v) = \frac{7}{4}(1-3v^2)\times k_2(v)$
- Triweight $k_{4,3}(v) = \frac{27}{16}(1-\frac{11}{3}u^2)\times k_3(v)$
- Gaussian $k_{4,gauss}(v) = \frac{1}{2}(3-u^2)\times k_{gauss}(v)$

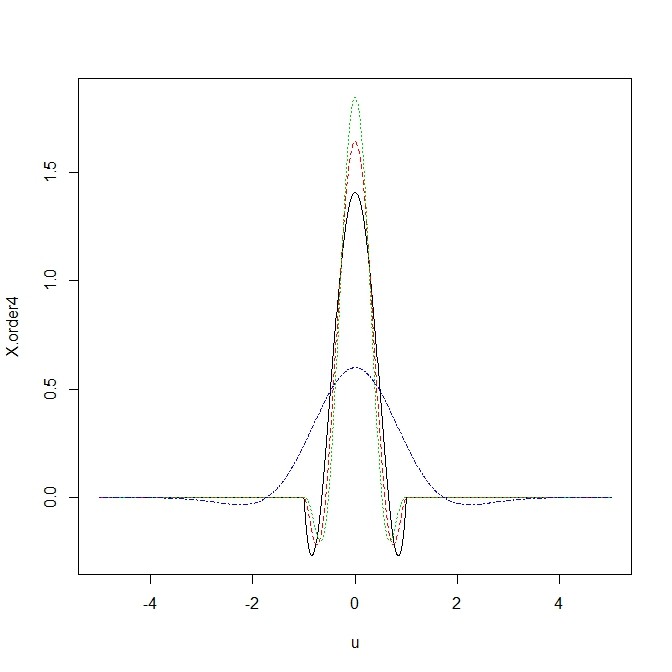
さらに6-th orderカーネルは…
- Epanechnikov $k_{6,1}(v) = \frac{175}{64}(1-6v^2+\frac{33}{5}v^4)k_1(v)$
- Biweight $k_{6,2}(v) = \frac{315}{128}(1-\frac{22}{3}v^2+\frac{143}{15}v^4)k_2(v)$
- Triweight $k_{6,3}(v) = \frac{297}{128}(1-\frac{26}{3}v^2+13v^2)k_3(v)$
- Gaussian $k_{6,gauss}(v) = \frac{1}{8}(15-10v^2+v^4)k_{gauss}(v)$

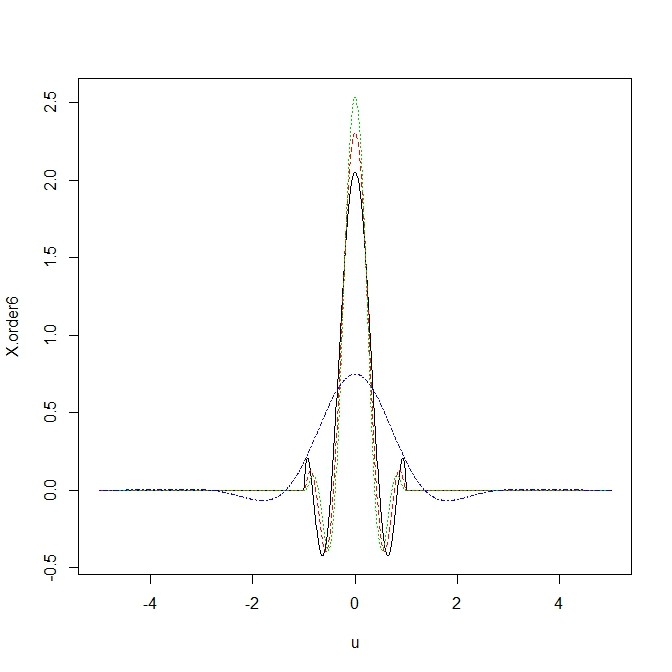
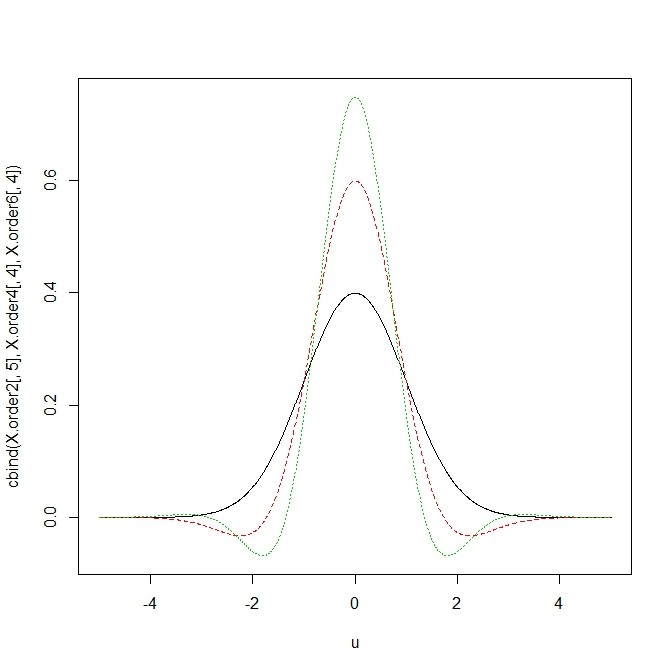
Gaussian-basedカーネルの2nd, 4th, 6th オーダーカーネルを重ねてプロットしてみる
- 実際、Gaussian-based カーネルの2r-th order関数は、2nd order gaussian kernel ()の導関数を用いて以下のような形をして表現される(参考こちら)
  - $k_{2r,gauss}=\frac{(-1)^r*k_{gauss}^{(2r-1)}(v)}{2^{r-1}(r-1)!x}$

k0 <- function(u){ # Uniform
	ret <- rep(0,length(u))
	a <- which(abs(u)<=1)
	ret[a] <- 1/2
	ret
}
k1 <- function(u){ # Epanchnikov
	ret <- rep(0,length(u))
	a <- which(abs(u)<=1)
	ret[a] <- 3/4 * (1-u[a]^2)
	ret
}
k2 <- function(u){ # Biweight
	ret <- rep(0,length(u))
	a <- which(abs(u)<=1)
	ret[a] <- 15/16 * (1-u[a]^2)^2
	ret
}
k3 <- function(u){ # Triweight
	ret <- rep(0,length(u))
	a <- which(abs(u)<=1)
	ret[a] <- 35/32 * (1-u[a]^2)^3
	ret
}
k.gauss <- function(u){ # Gaussian
	ret <- 1/sqrt(2*pi) * exp(-u^2/2)
	ret
}

u <- seq(from=-5,to=5,length=1000)
X.order2 <- matrix(0,length(u),5)
X.order2[,1] <- k0(u)
X.order2[,2] <- k1(u)
X.order2[,3] <- k2(u)
X.order2[,4] <- k3(u)
X.order2[,5] <- k.gauss(u)

matplot(u,X.order2,type="l")

k4.1 <- function(u){
	15/8*(1-7/3*u^2)*k1(u)
}
k4.2 <- function(u){
	7/4*(1-3*u^2)*k2(u)
}
k4.3 <- function(u){
	27/16*(1-11/3*u^2)*k3(u)
}
k4.gauss <- function(u){
	1/2*(3-u^2)*k.gauss(u)
}

X.order4 <- matrix(0,length(u),4)
X.order4[,1] <- k4.1(u)
X.order4[,2] <- k4.2(u)
X.order4[,3] <- k4.3(u)
X.order4[,4] <- k4.gauss(u)
matplot(u,X.order4,type="l")

k6.1 <- function(u){
	175/64*(1-6*u^2+33/5*u^4)*k1(u)
}
k6.2 <- function(u){
	315/128*(1-22/3*u^2+143/15*u^4)*k2(u)
}
k6.3 <- function(u){
	297/128*(1-26/3*u^2+13*u^4)*k3(u)
}
k6.gauss <- function(u){
	1/8*(15-10*u^2+u^4)*k.gauss(u)
}

X.order6 <- matrix(0,length(u),4)
X.order6[,1] <- k6.1(u)
X.order6[,2] <- k6.2(u)
X.order6[,3] <- k6.3(u)
X.order6[,4] <- k6.gauss(u)
matplot(u,X.order6,type="l")


matplot(u,cbind(X.order2[,5],X.order4[,4],X.order6[,4]),type="l")