Association Ruleの視覚化パッケージarulesViz - ryamadaの遺伝学・遺伝統計学メモ

arulesパッケージとarulesVizパッケージとを使ってAssociation Rule法の出力の中身とその視覚化について確認します。
以下はRmdファイルです。こちらなどを参考にすれば、自由にhtml文書化・epub化できます(が、それが面倒な場合には、kindleで→こちら)

メモ
- １行に１回の買い物アイテムセットがタブ区切りで入っているテキストファイルを読み込んでarulesの買い物情報オブジェクト(transactionsオブジェクト)を作る。
- 複数の入力ファイルがあるときには、ファイルを連結してから読み込ませる必要がある(もしアイテムリストが揃っていればmerge(my.trans1,my.trans2)のようにtransactionsオブジェクトのレベルで結合する関数もあるようだが…)

library(arules)
my.trans1 <- read.transactions("data1.txt",sep="\t",format="basket")

# 関連ルール法 Association Rule法をRでいじってみる
========================================================

スーパーマーケットでの買い物を考えてみよう。
色んな人が来ては、色んなアイテムを買っていく。
そのときに何を何と一緒に買うかには、それなりの意味が込められている。
たとえば、「ジャガイモと人参と玉ねぎとカレールー」という組合せとか、「食パンと牛乳とインスタントコーヒーとオレンジ」とか。

そんな１度の買い物で一緒になるアイテムをひたすらストックして行って、そこから、アイテム間に関係を見出そう、という方法がAssociation Rule learning法。
Wikipediaはhttp://en.wikipedia.org/wiki/Association_rule_learning 。

## Association ruleの「きほんのき」

買い物を行、アイテムを列とした{0,1}の行列がデータである。

アイテムの部分集合が2個あって、$X=\{x_1,x_2,...,x_{nx}\},Y=\{y_1,y_2,...,y_{ny}\}$とする。
$nx, ny \ge 1$である。

今、Xを買っているときには、必ずYも買っているとする。
ただし、XとYにはかぶりがない($X \cap Y = \phi$)とする。

そのとき、"Xという部分集合を買うならば、Yという部分集合も買う"と言えるが、このようなXとYの関係を見つけ、それを「ルール」と呼ぶ。

そして、そのルールにおいてXをantecedent(left-hand-side, LHS)と呼び、Yをconsequent(right-hand-side,RHS)と呼ぶ。

簡単な例でやってみよう。

```{r}
D <- matrix(c(1,1,0,0,0,0,1,0,0,0,0,1,1,1,1,1,0,1,0,0,0,1,1,1),byrow=TRUE,6,4)
D
```
行が買い物、列がアイテムである。

第2,3列の両方が1になっているのは、第4行と第6行である。

その第4,6行では、第2,3列のアイテム以外では、そろって第4列のアイテムが買われている。

したがって、X={第2アイテム,第3アイテム}を買うならば、Y={第4アイテム}は必ず一緒に買われている、と読める。

したがって、LHSをX={第2アイテム,第3アイテム}とし、RHSをY={第4アイテム}とするルールが見つかったことになる。

実際のルールの検出には、Xなら「必ず」Yというところに少し緩みを入れたりもするが、原則はこのような感じである。

お勉強はひとまず横に置き、ひとまずRでいじってみよう。

## RでのAssociation Rule
```{r}
install.packages("arulesViz") # arulesという基本パッケージもインストールされるはず
library(arulesViz)
```

Wiki記事にもあるように、ルールの検出アルゴリズムは複数ある。
* Aprioriアルゴリズム
* Eclatアルゴリズム
* FP-growthアルゴリズム
* その他(Node-set-basedアルゴリズム)
* GUHA procedure ASSOC
* OPUS search

そのうちの、Aprioriアルゴリズム。
```{r}
# これはデータ
# Michael Hahsler, Kurt Hornik, and Thomas Reutterer (2006) Implications of probabilistic data modeling for mining association rules. In M. Spiliopoulou, R. Kruse, C. Borgelt, A. Nuernberger, and W. Gaul, editors, From Data and Information Analysis to Knowledge Engineering, Studies in Classification, Data Analysis, and Knowledge Organization, pages 598???605. Springer-Verlag.より
data(Groceries)
# ちょっと中味を覗く
str(Groceries)
# 9835回分の買い物、169アイテムからなる
# 行に買い物、列にアイテムが0,1行列(0は.、1は|)になっている
Groceries@data[1:10,1:20]
# 買い物アイテムは、169行あり、3列になって階層的な説明がなされている
head(Groceries@itemInfo)
```

自前のデータをテキストファイルで持っているときには
```{}
バナナ  オレンジ  ヨーグルト
食パン  ハム
砂糖  イチゴ  ヨーグルト
```
というようなファイル(ここではタブ区切り)が"data1.txt"という名前だとしたら
```{}
my.data1 <- read.transactions("data1.txt",sep="\t",format="basket")
```
のようにして読み込む。最後のformat="basket"は、1行が1回の買い物に相当し、アイテムを並べている、というファイル形式である、ということを示す引数である。
# ルールを引きだす〜Aprioriアルゴリズム〜

基本的なアルゴリズム"Aprioriアルゴリズム"を使ってルールを引き出してみる。
```{r}
rules <- apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
rules
```
5668個のルールが見出されたことがわかる。

このrulesの中身を調べてみる。
rulesの主な出力は、169個のアイテムの部分集合の束。
```{r}
str(rules)
str(rules@lhs)
```

このrules@lhs@dataが169行5668列であるから、各列がルールで、各列は個々のルールの構成アイテムを表していることがわかる。
lhsであるからルール"X => Y"のXに当たるアイテムのリストである。


```{r}
rules@lhs@data[1:10,1:20]
```

同様にY(RHS)のは
```{r}
rules@rhs@data[1:30,1:20]
```
に格納されている。

ルールを構成するアイテム名を呼び出すには以下のようにする。

```{r}
# X LHSの場合
rules@lhs@itemInfo[rules@lhs@data[,1],1]
# Y RHSの場合
rules@rhs@itemInfo[rules@rhs@data[,1],1]
```

したがって、いくつかのルールを示すことにすれば、

```{r}
for(i in 1:5){
  tmp <- paste(paste("'",rules@lhs@itemInfo[rules@lhs@data[,i],1],"'",sep=""),"=>",paste("'",rules@rhs@itemInfo[rules@rhs@data[,i],1],"'",sep=""))
	print(tmp)
}
```

## ルールの重み〜サポートとコンフィデンスとリフト〜

たくさんの買い物で繰り返し認められるルールは信用性が高いだろう。
それを定量化するのがサポートである。

全部で$n$回分の買い物をしたときに、あるルールのLHS,Xが$n_x$回の買い物に登場したのなら、サポートは$\frac{n_x}{n}$となる。

もう一つの指標がコンフィデンスである。$n_x$回登場したXに対して、いつも必ずYが買われるならばコンフィデンスは1。ある割合で買われるなら、その割合がコンフィデンスである。

この関係を式で書くと
$$
\begin{equation}
supp(X) = \frac{nx}{x}\\
conf(X => Y) = \frac{supp(X \cup Y)}{supp(X)}\\
\end{equation}
$$

また、もう一つの指標がリフトである。
$$
lift(X => Y)=\frac{supp(X\cup Y)}{supp(X) \times supp(Y)}
$$

Rに話を戻せば、これらは、出力rulesにはその値が付いてきている。

```{r}
rules@quality[1,]
```

たくさんのルールができたが、ルールに何度も登場するアイテムと登場しないアイテムとがある。
この集計をしてみる。

各アイテムが、LHS、RHSに何回登場したかを数えてみる。
```{r}
n.LHS <- apply(rules@lhs@data,1,sum)
n.RHS <- apply(rules@rhs@data,1,sum)
# ルールに１度でも登場した回数
## LHS
length(which(n.LHS>0))
## RHS
length(which(n.RHS>0))
```
RHSに現れるアイテム数はかなり少ないことがわかる。

```{r}
# 分布をみてみる
h <- hist(c(n.LHS,n.RHS),plot=FALSE)
h <- hist(n.LHS,density=20,breaks=h$breaks,ylim=c(0,max(h$counts)))
hist(n.RHS,col=2,density=17,breaks=h$breaks,ylim=c(0,max(h$counts)),add=TRUE)

# LHSとRHSとの登場回数との間の関係をプロット
plot(n.LHS,n.RHS)
```

## ルールを構成するアイテムの間の関係を視覚化する

### ルールの指標の分布を視覚化する
全ルールをそのサポートとコンフィデンスとリフトの値によって、どんなルールが見つかったかをプロットする。
サポートを横軸、コンフィデンスを縦軸、リフトで明暗を分けている。

```{r}
## scatterplot
plot(rules)
## liftが決めるグラデーションを段階に分けると…
plot(rules, shading="order")
```

### アイテムの登場パターンを視覚化する

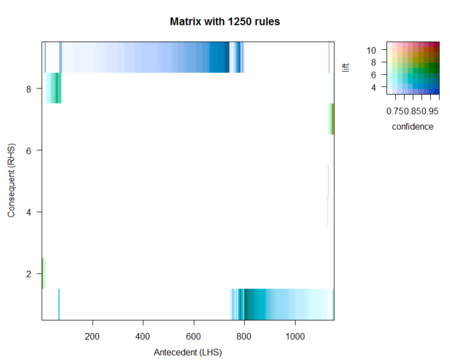
LHSとRHSに現れる様子を二次元表示する。

表示の指標はリフトとし、それを濃淡で表すことにする。

すべてのルールがプリントアウトされてしまうのだが…そこは適当に無視し欲しい。

```{r,}
## 2D matrix with shading
plot(rules, method="matrix", measure="lift",echo=FALSE)
```

ルールの数が多いと、一部の描図のために時間がかかるので、confidence値の高い方に限定しておく。
```{r}
subrules <- rules[quality(rules)$confidence > 0.7]
plot(subrules, method="matrix", measure="lift")
```
アイテムを適当に並べ替えて、シグナルがかたまるようにする。
```{r}
plot(subrules, method="matrix", measure="lift", control=list(reorder=TRUE))
```

2つの指標を反映させる異にする。
色具合と明度で実施する
```{r}
plot(subrules, method="matrix", measure=c("lift", "confidence"),   control=list(reorder=TRUE))
```

### ルールをグループ分けして視覚化する

対象は全ルールに戻して実施する。
オオマカニ言うと、LHSの方はたくさんのアイテムが採用され、多様性が高いのに対して、RHSの方がアイテム数が限定している。

ルールをグループ分けするなら、LHSの方をグループ分けしたい。

色々なアイテムで構成される部分集合がたくさんあるわけであるが、それらを、共通するアイテムでLHSをグループにしてやる方法が以下のプロットである。

「少なくともx1を買うならば、Yを買う」という意味になっている。

円の大きさがサポートを、色具合がliftを表している。

```{r}
## デフォルトでは20グループにまとめている
plot(rules, method="grouped")
# グループ数をk=10,30に指定している
plot(rules, method="grouped", control=list(k=10))
plot(rules, method="grouped", control=list(k=30))
```

## 特定のルールについてグラフ表示する

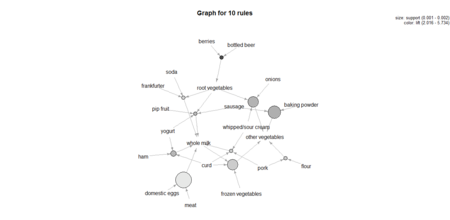
アイテム間がルールによってどのように結びついているかをグラフオブジェクトで表示してみる。

複雑な関係の視覚化方法である。したがって、ルール数は少なくしておく必要がある。
以下では、ランダムに10ルールを選んで実施している。

```{r}
## graphs only work with very few rules
subrules2 <- sample(rules, 10)
plot(subrules2, method="graph")
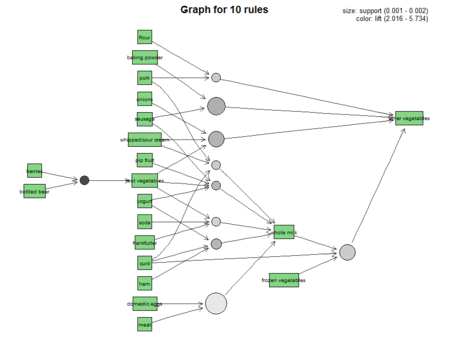
plot(subrules2, method="graph", 
	control=list(type="items"))
```

インターラクティブに動かせるプロット。
```{r}
plot(subrules2, method="graph", interactive=TRUE)
```

Graphvizにつないで、ちょっと豪華にプロット。
```{r}
plot(subrules2, method="graph", control=list(engine="graphviz", type="items"))
```
その他。
```{r}
#あまり面白くないかも…
plot(subrules2, method="paracoord")
plot(subrules2, method="paracoord", control=list(reorder=TRUE))
```

### 個別のルールについてその中身を知るための視覚化

一つのプロットがルール集の中でどのような意味合いになるのかを視覚化する。
適当にルールを選んでプロットする。

```{r}
oneRule <- sample(rules, 1)
plot(oneRule, method="doubledecker", data = Groceries)

## お試し。あまり面白くない…
install.packages("iplots")
library(iplots)
sel <- plot(rules, method="iplots", interactive=TRUE)
```

## Eclatアルゴリズムの出力とその視覚化

eclatアルゴリズムはaprioriアルゴリズムが幅優先探索であるのに対して、深さ優先探索アルゴリズムである。

「併せて買われるアイテムの部分集合」を基準に照らして取り出す手法である。
```{r}
## for itemsets
itemsets <- eclat(Groceries, parameter = list(support = 0.02))
itemsets
```
122ルールが見出されたことがわかる。

```{r}
str(itemsets)
dim(itemsets@items@data)
```
これにより、行にアイテム、列にルールという行列のありかがわかる。
中味を覗けば、0,1(0は.、1は|)の行列であるとわかる。

```{r}
head(itemsets@items@data)
```

これをグラフオブジェクトでプロットする。

円がルールを表し、その大きさがサポートの強さを表している。
ルールにはアイテムが帰属しているので、アイテムからの矢印が描かれている。

アイテムは一度しか描かれないので、同じアイテムを含むルール同士は近い位置に配置されることとなる。

全ルールを視覚化するとこのようになる。
```{r}
plot(itemsets, method="graph")
```
40個のルールを適当に選んで描いてみると以下のようになる。

```{r}
subitemsets <- sample(itemsets, 40)
plot(subitemsets, method="graph")
```