2011-12-03

分割表の位置・自由度・座標変換４　分割表の正単体・複体座標表現

多次元分割表の尺度別カテゴリ数が $\mathbf{r}=\{r_1,r_2,...,r_k\};r_i \in \mathbf{Z}$ であるときの、表のセルの総数は $R=\prod_{i=1}^k r_i$ である
このような表にの行列を次のように与える
- $k$ 個の尺度の集合のべき集合の $2^k$ 個の要素 $p_i \in P_{ow}(A)$ ごとに、それらが作る複合カテゴリ $\prod_{j=1} {n_1} r_{i_j}$ 個に対応させた、長さ $\prod_{j=1} {n_1} (r_{i_j}-1)$ のベクトルが算出されている
- 元の $k$ 次元分割表の $R$ 個のセルは $\prod_{j=1} {n_1} r_{i_j}$ 個の複合カテゴリのいずれかに対応するので、それぞれのセルに対応する長さ $\prod_{j=1} {n_1} (r_{i_j}-1)$ のベクトルを与える
- これにより、 $(\prod_{j=1} {n_1} (r_{i_j}-1)) \times R$ の行列ができる
- このようにしてできる行列をすべての $p_i$ に関して連ねることで、 $R \times R$ 行列 $X$ ができる。ただし、上記では、 $P_{ow}(A)$ の要素の一つである $\phi$ に対応する記載がないが、これは、すべての要素が1であるような長さ $R$ のベクトルであるとする
- これをRで算出する

# 尺度ごとのカテゴリ数を納めたベクトル
ns<-c(2,4)
# 各尺度のカテゴリを正単体に納めたときのその頂点座標
CV<-list()
for(i in 1:length(ns)){
	CV[[i]]<-CategoryVector(ns[i])
}
# 全セル数Rとそれを納めたアレイtとアレイの番地を納めた行列taddress
t<-array(1,ns)
taddress<-which(t>0,arr.ind=TRUE)
R<-prod(ns)
# 各尺度に対応する正単体座標をR個のセルのすべてに対応付ける(以降の計算の便のため)
CVext<-list()
for(i in 1:length(ns)){
	tmp<-matrix(0,length(CV[[i]][1,]),R)
	for(j in 1:R){
		tmp[,j]<-CV[[i]][taddress[j,i],]
	}
	CVext[[i]]<-tmp
}
# 尺度の組合せを網羅するために、集合にして、そのべき集合を作る
s<-as.set(1:length(ns))
ps<-set_power(s)
# Xはべき集合の要素ごとに頂点座標を格納
# YはXのすべてを１つの行列に納めてRxR行列にしたもの
X<-NULL
Y<-NULL
cnt<-1
# 全てのべき集合要素についてのループ
for(i in ps){
	#print(i)
# 空集合のときは、すべての要素が1である長さRのベクトル
	if(set_is_empty(i)){
		#print("null")
		tmpX<-rep(1,R)
	}else{
# それ以外の場合
# 冪集合要素をベクトルに納める
		tmplist<-c()
		for(j in i){
			tmplist<-c(tmplist,j)
		}
		N<-length(tmplist)
		tmpX<-NULL
# 尺度数が1なら、CVextそのものを納めればよい
		if(N==1){
			tmpX<-CVext[[tmplist]]
# そうでないときには、積を繰り返して、変数の数が増えていく
# それをすべてのセルについて逐一実施する
		}else{
			initX<-CVext[[tmplist[1]]]
			vals<-NULL
			for(j in 1:R){
				tmpvals<-initX[,j]
				print(tmpvals)
				for(k in 2:N){
					tmpvals<-outer(tmpvals,CVext[[tmplist[k]]][,j],FUN="*")
					#print(tmpvals)
				}
				tmpvals<-c(tmpvals)
# R個すべてのセルについて連結して、				vals<-rbind(vals,tmpvals)
			}
# 最後に出力用に納める
			tmpX<-t(vals)
		}
		
		
	}
	if(is.null(dim(tmpX)))tmpX<-matrix(tmpX,nrow=1)
	Y<-rbind(Y,tmpX)
	X[[cnt]]<-tmpX
	cnt<-cnt+1
}
# 出力を確認する
Y
X
# さて、適当なR次元ベクトルを作る
v2<-runif(R)
# それを座標変換する
P<-Y%*%v2
# ベクトルが、すべてのセルの期待値が1であるような多次元分割表の「観察-期待」値ベクトルであるとすれば、そのカイ自乗値は次のように計算できる
sum(v2^2)
# 変換した座標でも、計算できる
sum((solve(Y)%*%P)^2)

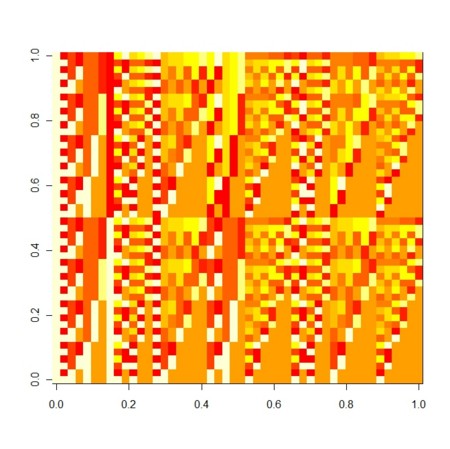
- ns=c(2,3,4,2)の場合のXのイメージを見てみよう